Progressão Geométrica


Vamos resolver uma questão envolvendo progressão geométrica do vestibular da UFRGS 2016.

A questão é:



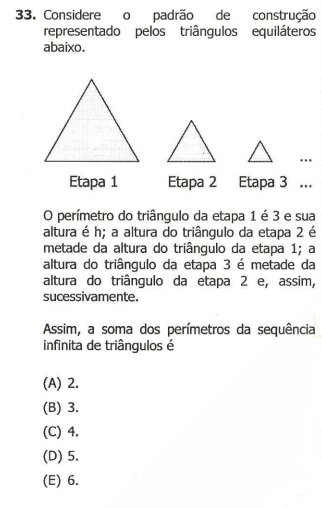
Essa questão trata-se de uma soma infinita de uma progressão geométrica, cuja fórmula é:

S_n = a₁/(1 - q)

Dados:

a₁ = 3
q = ?

A questão nos informa que a altura do triângulo da segunda etapa vale metade da altura do triângulo da primeira etapa. Então,:

h₂ = h₁/2

Todos os triângulos são equiláteros. Logo, a altura de todos será dado por:

h = (L √ 3)/2

Mas o lado do primeiro triângulo vale 1, já que o perímetro (soma dos lados) vale 3. Portanto,

h₁ = (1 √ 3)/2

Com isso, o valor de h₂ será:

h₂ = h₁/2
h₂ = [( √ 3)/2]/2
h₂ = ( √ 3)/4

Agora que temos o valor de h₁ e h₂, podemos calcular o valor de q:

q = h₂/h₁
q = [( √ 3)/4]/[( √ 3)/2)]
q = 1/2

Com o valor de q em mãos, vamos calcular a soma infinita:

S_n = a₁/(1 - q)
S_n = 3/(1 - (1/2))
S_n = 3/(1/2)
S_n = 6

Então, o valor de S_n será igual a 6.

ALTERNATIVA E

---

Questão Anterior

Página Principal

Questão Posterior