Geometria Plana

Vamos resolver uma questão envolvendo geometria plana do vestibular da FUVEST 2001 - 1ª fase.

A questão é:



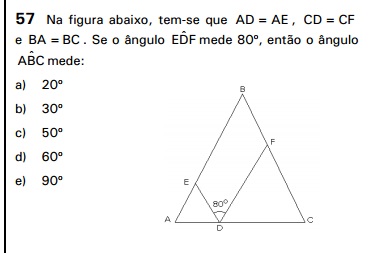
Vamos redesenhar a figura da questão:



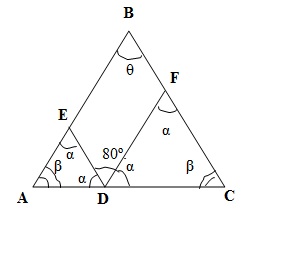
Observe ao redor do ponto D. A soma dos ângulos α com 80^o é igual a 180^o.

Logo,

α + 80^o + α = 180^o
2 . α + 80^o = 180^o
2 . α = -80^o + 180^o
2 . α = 100^o
α = 100^o/2
α = 50^o

No triângulo Δ ADE, a soma dos ângulos internos vale 180^o.

Portanto,

2 . α + β = 180^o

Mas, α = 50^o.

Então,

2 . α + β = 180^o
2.50^o + β = 180^o
100^o + β = 180^o
β = 180^o - 100^o
β = 80^o

No Δ triângulo ABC, a soma dos ângulos internos também vale 180^o.

Logo,

2 . β + θ = 180^o

Mas, β = 80^o.

Então,
2. β + θ = 180^o
2.80^o + θ = 180^o
160^o + θ = 180^o
θ = 180^o - 160^o
θ = 20^o

Portanto, o ângulo em B vale θ = 20^o

ALTERNATIVA A.

---

Questão Anterior

Página Principal

Questão Posterior