Geometria Plana

Vamos resolver uma questão envolvendo geometria plana do vestibular da FUVEST 2001 - 1ª fase.

A questão é:



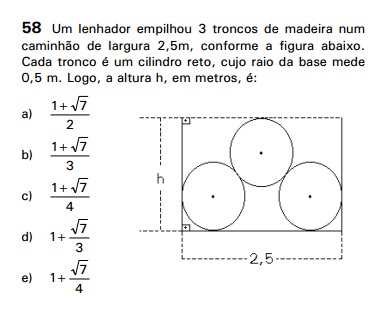
Vamos redesenhar a figura da questão:



Observando a figura, concluímos que:

- o lado AB = AC = 1
- o lado BC = 1,5
- o triângulo Δ ABC é isósceles.

Usando Pitágoras para o triângulo Δ ADC, teremos:

x² + (0,75)² = 1²
x² + (3/4)² = 1²
x² + (9/16) = 1²
x² = 1 - 9/16
x² = 7/16
x = √ (7/16)
x = √ 7/4

Veja que a altura h é composta por 2 raios de circunferência mais o valor de x. Então.

h = 0,5 + 0,5 + x
h = 1 + x
h = 1 + √ 7/4

Portanto, a altura h vale 1 + √ 7/4

ALTERNATIVA E.

---

Questão Anterior

Página Principal

Questão Posterior