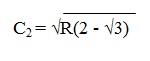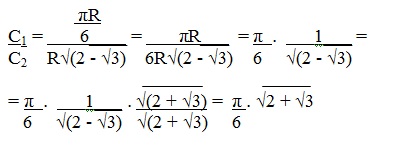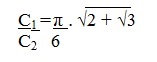Geometria Plana

Vamos resolver uma questão envolvendo geometria plana do vestibular da FUVEST 2001 - 1ª fase.

A questão é:



Vamos redesenhar a figura abaixo:



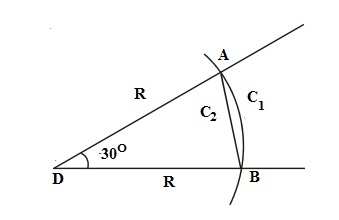
Uma circunferência completa tem 2 π R. Já o arco C₁ tem o seguinte comprimento:

C₁ = ( π /6)R

Usando a lei dos cossenos no triângulo Δ ABD, para encontrar o valor de C₂, vamos ter:

C₂² = R² + R² - 2.R.R.cos ( π /6) =

C₂² = 2R² - 2.R.R. ( √ 3/2) =

C₂² = 2R² - R² √ 3 =

C₂² = R²(2 - √ 3)




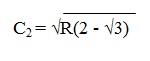
Fazendo a razão C₁/C₂, teremos:




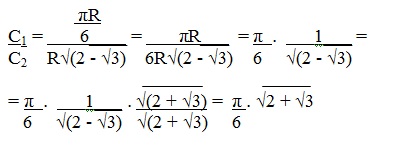
Logo, a razão C₁/C₂ vale:



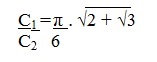
ALTERNATIVA C

---

Questão Anterior

Página Principal

Questão Posterior