
Geometria Plana
Vamos resolver uma questão envolvendo geometria plana do vestibular da FUVEST 2001 - 1ª fase.
A questão é:
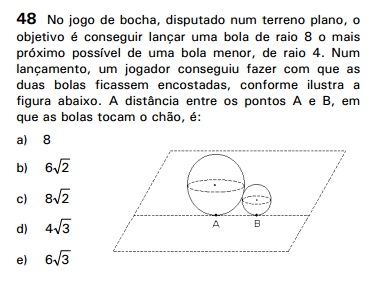
Vamos redesenhar as duas bolas do ponto de vista de uma pessoa que esteja exatamente acima delas e acrescentaremos os dados fornecidos pela
questão:
Observando a figura, vemos que existe um triângulo retângulo OQP. Já que ele é retângulo, podemos aplicar Pitágoras.

Então,
(OP)2 = (OQ)2 + (QP)2
Dados:
OP = 4 + 8 = 12
OQ = 4
QP = x
Substituindo em (OP)2 = (OQ)2 + (QP)2:
(OP)2 = (OQ)2 + (QP)2
122 = 42 + x2
144 - 16 = x2
x2 = 128
x = 8 √ 2
Veja que o valor de x é o mesmo da distância AB da figura. Portanto, a distância entre os pontos A e B vale 8 √ 2.
ALTERNATIVA C
Questão Anterior
Página Principal
Questão Posterior



