
O Cilindro
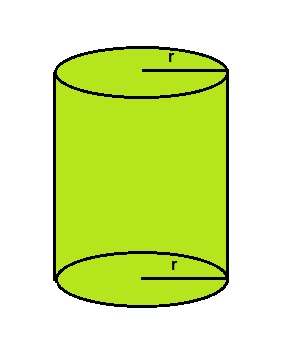
Definição:
O cilindro é um poliedro gerado pela rotação completa de um retângulo por um de seus lados.

Cilindros oblíquos e retos

Elementos de um cilindro

bases - áreas A1 e A2
altura h
geratriz - qualquer reta pertencente a área lateral delimitada pelas duas circunferências do cilindro.
Secção
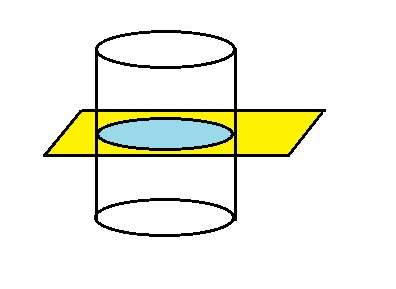
A secção transversal é determinada pela intersecção do plano paralelo às bases com o cilindro.
Todas essas secções são congruentes.
Secção Meridiana
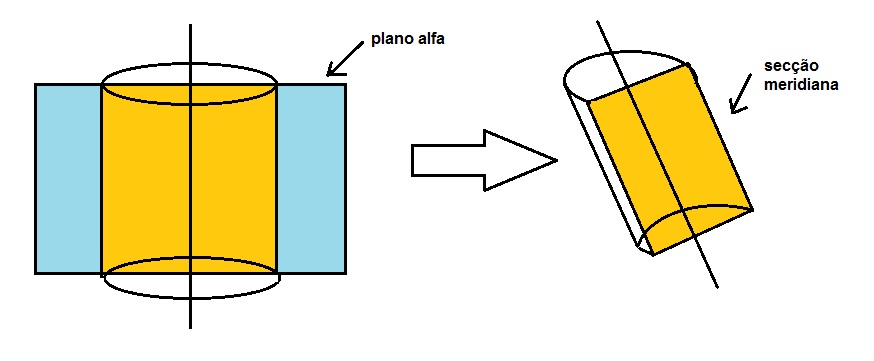
É aquela intersecção do cilindro que contém o meridiano.
Cilindro Equilátero

Quando a secção meridiana for um quadrado, dizemos que o cilindro é equilátero.
Áreas do cilindro
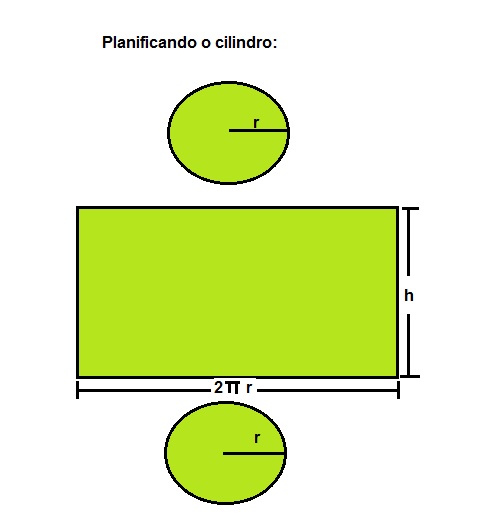
- Área lateral:
A área lateral de um cilindro é um retângulo cujas dimensões são 2πr e h
Logo, AL = 2πr.h
- Área da base:
Essa área é formada pela base que é um círculo. Logo, AB = πr2
- Área total:
A área total é soma da área lateral com as duas bases do cilindro. Portanto,
AT = AL + 2.AB
AT = 2πr.h + 2.πr2
AT = 2πr(h + r)
Volume de um cilindro

V = AB.h
V = π.r2.h
Exercício:
(VUNESP-SP) Num tonel de forma cilíndrica esté depositada uma quantidade de vinho que ocupa a metade de sua capacidade. Retirando 40L de seu conteúdo, a altura do nível do vinho baixa 20%. O número que expressa a capacidade desse tonel, em litros, é:
a) 200
b) 300
c) 400
d) 500
e) 800
Solução:
A metade do volume do tonel é:
V/2 = π.r2.(h/2)
Quando retiramos 40 litros e a altura cai em 20%, teremos:
V/2 - 40 = π.r2 - 0,8h
Mas V/2 = π.r2.(h/2). Logo,
V/2 - 40 = π.r2 - 0,8(h/2)
π.r2.(h/2) - 40 = π.r2 - 0,8(h/2)
π.r2.(h/2) - π.r2 - 0,8(h/2) = 40
π.r2.0,2(h/2) = 40
π.r2.0,2.h = 40.2
π.r2.h = 80/0,2
π.r2.h = 400
Mas π.r2.h = V. Então,
π.r2.h = 400
V = 400 litros
ALTERNATIVA C
Próxima Aula
Aula Anterior
Página do Capítulo
Página do Curso
Página Principal