
O Cubo

Definição:
O cubo é um paralelepípedo cujas arestas são congruentes (do mesmo tamanho). As seis faces do cubo são quadrados.
Diagonais do cubo e da base
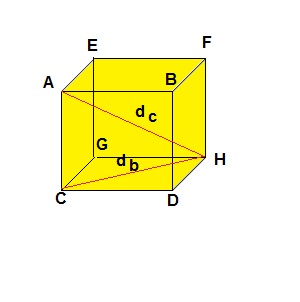
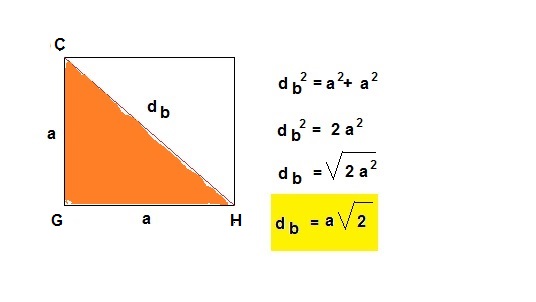
- Diagonal da base:
- Diagonal do cubo:

Área lateral de um cubo

Área Total

Volume
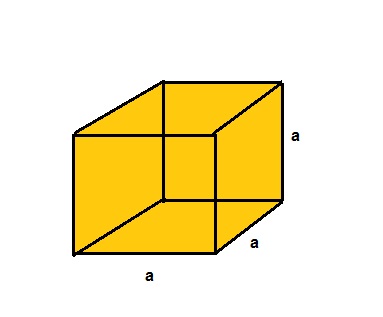
O cubo é um paralelepído. Logo, seu volume será a multiplicação das suas dimensões e elas são iguais, teremos:
V = a.a.a = a3
Logo, V = a3
Exercício:
(FUVEST-SP) A aresta do cubo abaixo mede 2 e a reta BP mede 3. Calcule PC e PD.
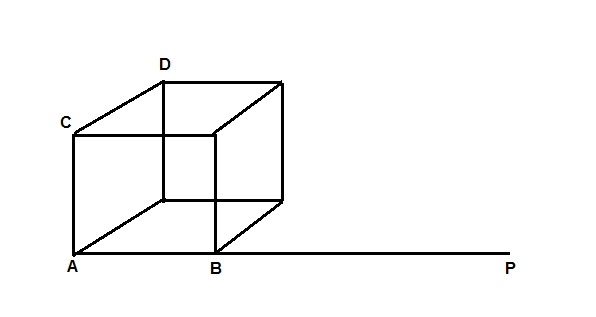
Solução:
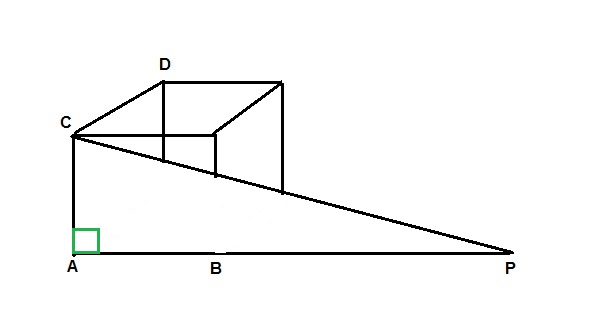
PC é a hipotenusa do triângulo PAC. Logo, aplicando o Teorema de Pitágoras, seu valor será:
(PC)2 = (AB + BP)2 + (AC)2
Dados:
AB = 2
BP = 3
AC = 2
Então,
(PC)2 = (AB + BP)2 + (AC)2
(PC)2 = (2 + 3)2 + 22
(PC)2 = 52 + 22
(PC)2 = 25 + 4
(PC)2 = 29
(PC)2 = √29
Para calcular PD, devemos observar o triângulo PCD:

Dados:
PC = √29
CD = 2
Aplicando Pitágoras, teremos:
(PD)2 = (PC)2 + (CD)2
(PD)2 = (√29)2 + 22
(PD)2 = 29 + 4
(PD)2 = 33
PD = √33
Próxima Aula
Aula Anterior
Página do Capítulo
Página do Curso
Página Principal