
Posição de Um Ponto em Relação a Uma Circunferência
Definição:
Dada a equação da circunferência (x - a)2 + (y - b)2 = r2 e um ponto P(m,n), podemos relacioná-los da seguinte forma:
- P está fora da circunferência:
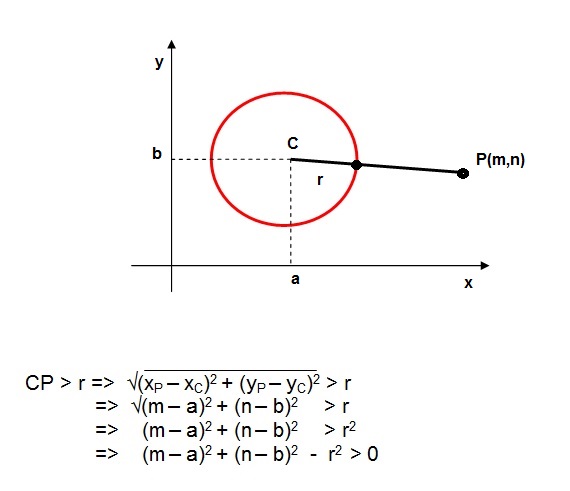
- P pertence à circunferência:
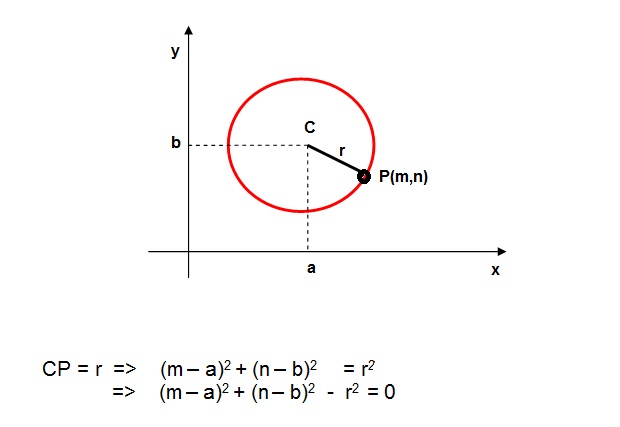
- P está dentro da circunferência:
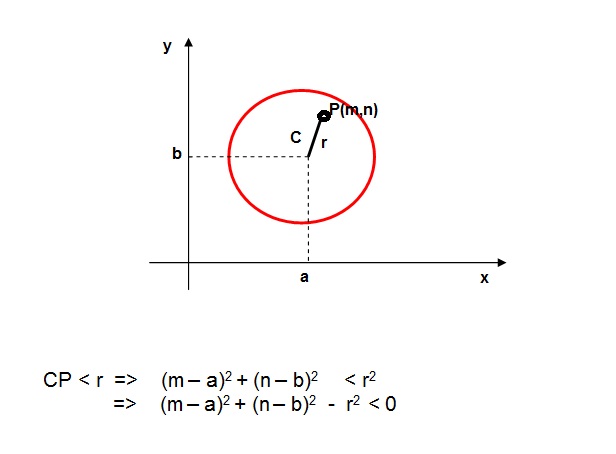
Exercícios:
1) (UFJF) Considere a circunferência C: (x - 1)2 + (y + 3)2 = 9
Determine se o ponto A(4, -3) é interior, exterior ou pertencente à circunferência.
Solução:
Temos que o raio r2 = 9. Logo,
r2 = 9
r = √9
r = 3
Dados da questão:
a = 1
b = -3
m = 4
n = -3
Então,
(m - a)2 + (n - b)2
(4 - 1)2 + (-3 + 3)2
32 + 02
9
Portanto, CP = r, pois
(m - a)2 + (n - b)2 - r2 = 0
9 - 9 = 0
Logo, o ponto P pertence à circunferência.
2) (FGV) No plano cartesiano, considere a circunferência de equação x2 + y2 - 4x = 0 e o ponto P(3,√3).
Verificar se P é interior, exterior ou pertencente à circunferência.
Solução:
Temos que:
-2a = -4
2a = 4
a = 4/2
a = 2
-2b = 0
-b = 0
b = 0
a2 + b2 - r2 = 0
22 + 02 - r2 = 0
4 + 0 - r2 = 0
-r2 = -4
r2 = 4
r = √4
r = 2
Pela questão temos que:
m = 3
n = √3
Logo,
(3 - 2)2 + (√3 - 0)2
12 + (√3)2
1 + 3
4
Portanto, CP = r, pois (m - a)2 + (n - b)2 - r2 = 0. Logo, o ponto P pertence à circunferência.
Próxima Aula
Aula Anterior
Página do Capítulo
Página do Curso
Página Principal