
Equação Geral da Circunferência
Definição:
A equação geral da circunferência é:
x2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0
Demonstração:
Da equação reduzida da circunferência , temos:
(x - a)2 + (y - b)2 = r2
Expandindo:
x2 - 2ax + a2 + y2 - 2by + b2 = r2
x2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0
Método para encontrar o centro e o raio da circunferência
Exemplo:
1) Encontre o centro e o raio da circunferência através da sua equação geral x2 + y2 - 8x + 12y + 16 = 0
Solução:
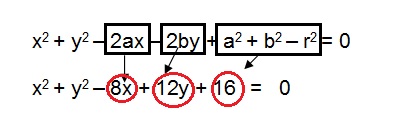
Logo,
-2a = -8 => -a = -8/2 => -a = -4 => a = 4
-2b = 12 => -b = 12/2 => -b = 6 => b = -6
a2 + b2 - r2 = 16
42 + (-6)2 - r2 = 16
16 + 36 - r2 = 16
52 - r2 = 16
-r2 = 16 - 52
-r2 = -36
r2 = 36
r = √36
r = 6 (raio é sempre positivo)
Portanto, o centro vale C(4,-6) e raio vale r = 6
Exercícios:
(UFRGS) A área do quadrado inscrito na circunferência de equação x2 - 2x + y2 = 0 vale:
a) 1
b) 1/2
c) 2
d) 4
e) 1/4
Solução:
Vamos reescrever a equação como:
x2 + y2 - 2x = 0
Então,
-2a = -2 => -a = -2/2 => -a = -1 => a = 1
-2b = 0 => -b = 0/2 = -b = 0 => b = 0
a2 + b2 - r2 = 0
12 + 02 - r2 = 0
1 + 0 - r2 = 0
-r2 = -1
r2 = 1
r = √1
r = 1 (raio é sempre positivo)
Observe o gráfico abaixo:

Veja que a diagonal do quadrado é igual ao diâmetro da circunferência. Logo,
diâmetro = diagonal
2.r = a√2 (onde "a" é o valor do lado do quadrado)
2.1 = a√2
2 = a√2
a = 2/√2
a = 2√2/[(√2).(√2)]
a = 2√2/2
a = √2
A área do quadrado é:
AQUADRADO = a2
AQUADRADO = (√2)2
AQUADRADO = 2
ALTERNATIVA C
Próxima Aula
Aula Anterior
Página do Capítulo
Página do Curso
Página Principal