
Posição de Uma Reta em Relação a Uma Circunferência
Definição:
Dada a equação da circunferência (x - a)2 + (y - b)2 = r2 e uma reta s: Ax + By + C, podemos relacioná-los da seguinte forma:

A distância do centro à reta detemina sua posição em relação à circunferência:

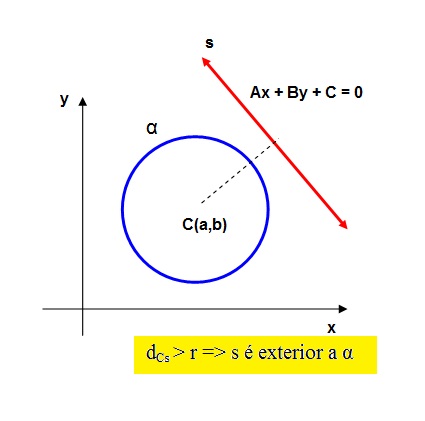

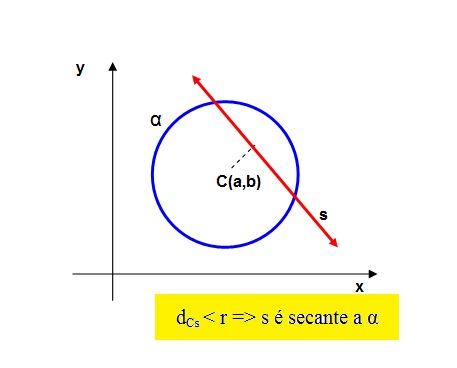
Exercício:
(MACK-SP) Em relação à circunferência (x - 1)2 + (y - 2)2 = 169, a reta 5x + 12y - 198 = 0 é:
a) secante
b) tangente
c) externa
d) coincidente com a reta que contém o diâmetro.
e) n.d.a.
Solução:
Chamaremos de reta s a equação: 5x + 12y - 198 = 0
Temos que:
r2 = 169
r = √169
r = 13
Vamos agora encontrar a distância do centro à reta:
Dados:
A = 5
B = 12
C = -198
a = 1
b = 2
Então,

Logo, dCs = r e a reta s é tangente à circunferência.
ALTERNATIVA B
Próximo Capítulo
Aula Anterior
Página do
Página do Curso
Página Principal