
Equação Reduzida da Circunferência
Definição:
Dado o centro C(a,b) e um ponto P(x,y) qualquer da circunferência, a distância de C a P será o raio dessa circunferência:


Portanto, a equação reduzida da circunferêcia será igual a:
(x - a)2 + (y - b)2 = r2
Observação:
Quando o centro da circunferência passa pela origem C(0,0), temos:
x2 + y2 = r2
Exercícios:
1) (UFRGS) A equação do círculo que passa na origem e tem coordenadas do centro o ponto P(-3,4) é:
a) (x + 3)2 + (y - 4)2 = 25
b) (x - 3)2 + (y + 4)2 = 25
c) x2 + y2 = 25
d) x2 + y2 = 5
e) (x - 3)2 + (y + 4)2 = 5
Solução:
Temos:
a = -3
b = 4
r = ?
Veja a figura abaixo:
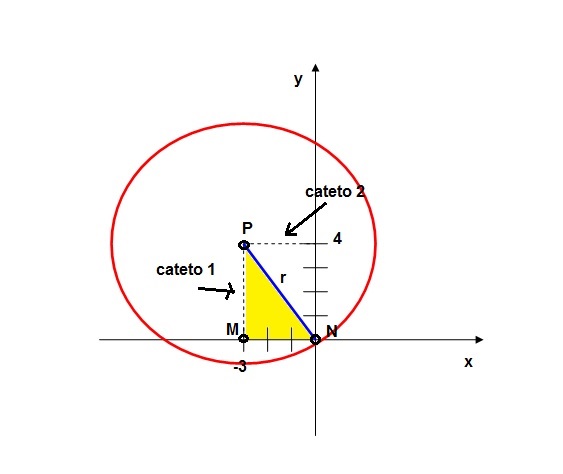
Vemos que o raio da circunferência é igual a hipotenusa do triângulo retângulo MNP. Logo,
r2 = (cateto 1)2 + (cateto 2)2
onde,
cateto 1 = -3
cateto 2 = 4
r2 = (-3)2 + 22
r2 = 9 + 16
r = √25
r = 5
Temos que a equação reduzida da circunferência vale:
(x - a)2 + (y - b)2 = r2
(x + 3)2 + (y - 4)2 = 52
(x + 3)2 + (y - 4)2 = 25
ALTERNATIVA A
2) (UFRGS) O triângulo equilátero está inscrito na circunferência como mostra a figura:

A equação da circunferência é:
a) x2 + y2 = 1/3
b) x2 + y2 = 4/3
c) x2 + (y - (2√3/3))2= 1/3
d) x2 + (y - (√3/6))2= 1/3
e) x2 + (y - (√3/3))2= 4/3
Solução:
Veja a figura abaixo:
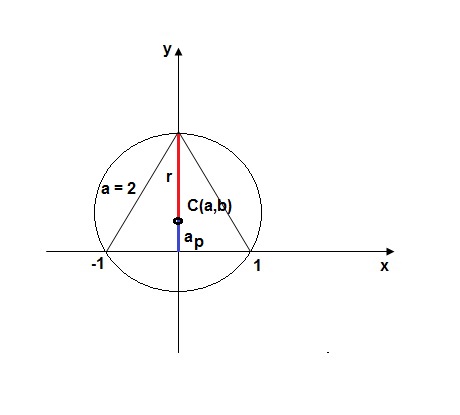
Da Geometria Plana sabemos que o lado do triângulo equilátero inscrito vale:
a = R√3
Pelo gráfico, temos que a = 2. Logo,
2 = R√3
2/(√3) = R
R = 2.(√3)/(√3.√3)
R = 2.(√3)/3
Para o centro, vemos que a = 0, pois a coordenada a está sobre o eixo y. O valor da coordenada b é igual ao apótema do
triângulo. Portanto,
b = ap = R/2
Mas R = 2.(√3)/3. Então,
ap = R/2 => R = [2.(√3)/3]/2 = (√3)/3
ap = (√3)/3
Portanto, b = (√3)/3
Temos que a equação reduzida da circunferência vale:
(x - a)2 + (y - b)2 = r2
(x - 0)2 + (y - √3/3 )2 = (2.(√3)/3)2
x2 + (y - √3/3 )2 = (4.3)/9)
x2 + (y - √3/3 )2 = 4/3
ALTERNATIVA E
Próxima Aula
Aula Anterior
Página do Capítulo
Página do Curso
Página Principal