
Área de um triângulo
Definição:
Dados três pontos A(xA, yA), B(xB, yB) e C(xC, yC), a área de um triângulo será dada por:


Exercícios:
1) (PUC-SP) As retas y = 2x, y = x/2 e x = 4 determinam um triângulo cuja área é:
a) 8
b) 10
c) 12
d) 16
e) 18
Solução:
Para achar a área do triângulo precisamos dos três vértices A, B e C. Para isso, vamos igualar as 3 equações
entre si.
Substituindo x = 4 em y = 2x, temos:
y = 2x
y = 2.4
y = 8
Logo, ponto A(4,8)
Substituindo x = 4 em y = x/2, temos:
y = x/2
y = 4/2
y = 2
Logo, ponto B(4,2)
Substituindo y = 2x em y = x/2 => x = 2y, temos:
y = 2x
y = 2(2y)
y = 4y
y - 4y = 0
5y = 0
y = 0/5
y = 0
Para y = 0, temos x = 2y => x = 2.0 => x = 0
Logo, C(0,0)
Substituindo os pontos A, B e C na fórmula da área do triângulo, teremos:
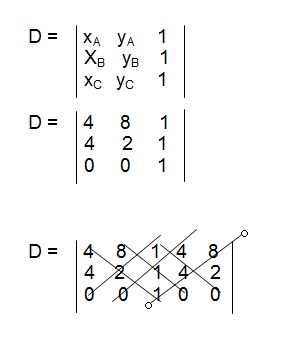
D = 4.2.1 + 8.1.0 + 1.4.0 - (0.2.1 + 0.4.1 + 1.4.8)
D = 8 + 0 + 0 - (0 + 0 + 32)
D = 8 - 32
D = -24
Portanto, a área será:
AT = (1/2).|D|
AT = (1/2).|-24|
AT = 24/2
AT = 12
ALTERNATIVA C
(FMU-SP) Dados os pontos A(-1,1), B(1,-1), C(2,1) e D(1,2), a área do quadrilátero ABCD é igual a:
a) 12
b) 10
c) 8
d) 9/2
e) 4
Solução:
Observe o gráfico abaixo:

A área do quadrilátero é formada por dois triângulos. Vamos calcular a área de cada um deles:
Área A1:
Temos os seguintes vértices: A(-1,1), B(1,-1) e D(1,2). Logo,

D = (-1).(-1).1 + 1.1.1 + 1.1.2 - (1.(-1).1 + 2.1.(-1) + 1.1.1)
D = 1 + 1 + 2 - (-1 - 2 + 1)
D = 4 - (-2)
D = 4 + 2
D = 6
A área A1 será:
A1 = (1/2).|D|
A1 = (1/2).6
A1 = 6/2
A1 = 3
Área A2:
Temos os seguintes vértices: B(1,-1) e D(1,2) e C(2,1). Logo,

D = 1.2.1 + (-1).1.2 + 1.1.1 - (2.2.1 + 1.1.1 + 1.1.(-1))
D = 2 - 2 + 1 - (4 + 1 - 1)
D = 1 - 4
D = -3
A área A2 será:
A2 = (1/2).|D|
A2 = (1/2).|-3|
A2 = 3/2
Portanto, a área total será A1 + A2 = 3 + 3/2 = (6 + 3)/2 = 9/2
ATOTAL = 9/2
ALTERNATIVA D
Próxima Aula
Aula Anterior
Página do Capítulo
Página do Curso
Página Principal