
Distância Entre Ponto e Reta
Definição:
Dados um ponto P(x1, y1) e a reta r: ax + by + c = 0. Definimos a distância entre a reta e o ponto P(x1, y1) como:
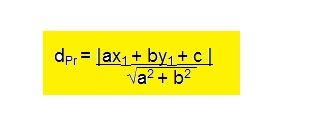
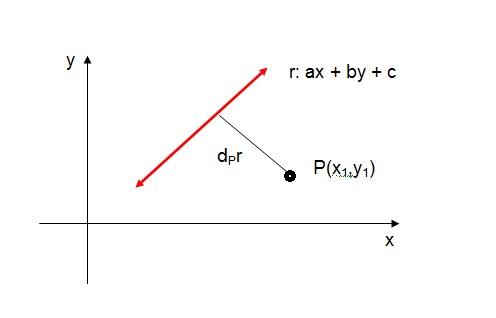
Exercícios:
1) (MACK-SP) A equação da reta paralela a y = x com distância √2 do ponto P(1,2) e que passa pelo 2o. quadrante é:
a) x - y + 3 = 0
b) x - y - 1 = 0
c) x - y - 2 = 0
d) x - y + 1 = 0
e) x - y + 2 = 0
Solução:
Definindo as retas r e s:
r: y = x
s: ?
Para a reta y = x, temos:
a = 1
b = -1
Como a reta r e s são paralelas, os coeficientes de r e s são iguais. Logo,
as = 1
bs = -1
Então, a reta s é iguai a:
x - y + c = 0
Sendo a distância até o ponto P igual a √2, temos:
x1 = 1
y1 = 2
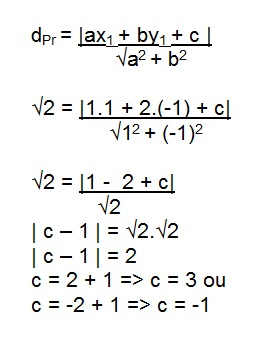
Para que a reta s passe pelo segundo quadrante, temos que ter c = 3.
Logo, a equação da reta s vale:
x - y + 3 = 0
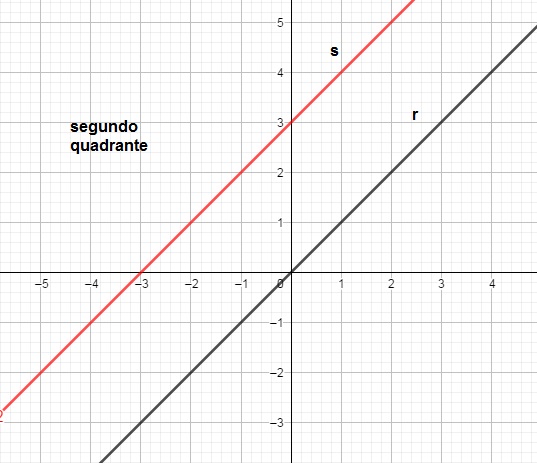
ALTERNATIVA A
2) (UFRGS) Considere a reta r passando em P(0, 3). Duas retas p e q, paralelas ao eixo das ordenadas e distantes entre si 2 unidades, são interceptadas no 1o. quadrante pela reta r em 2 pontos cuja distância é 2√5 unidades. A equação da reta r é:
a) y = 3x - 2
b) y = 2x + 3
c) 3x + y - 3 = 0
d) y = -2x - 3
e) 3x - y + 3 = 0
Solução:
Conforme os dados da questão, projetamos o gráfico abaixo:
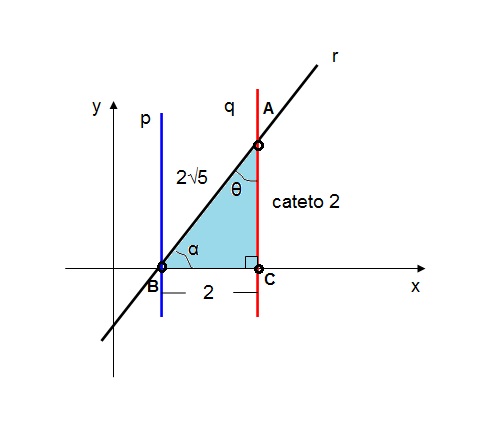
Observamos que o triângulo ABC é retângulo. Logo, podemos aplicar o Teorema de Pitágoras:
hipotenusa = 2√5
cateto 1 = 2
cateto 2 = ?
(hipotenusa)2 = (cateto 1)2 + (cateto 2)2
(2√5)2 = 22 + (cateto 2)2
4.5 = 4 + (cateto 2)2
20 - 4 = (cateto 2)2
(cateto 2)2 = 16
cateto 2 = √16
cateto 2 = 4
A tangente do ângulo θ vale:
tg θ = cateto oposto / cateto adjacente = (cateto 1)/(cateto 2)
tg θ =(cateto 1)/(cateto 2)
tg θ = 2/4
tg θ = 1/2
Aprendemos que quando uma das retas é vertical, temos:
tg θ = 1/tg α
Logo,
tg θ = 1/tg α
1/2 = 1/tg α
tg α = 2
Como tg α = mr é o coeficiente angular da reta r e ela passa pelo ponto P(0,3), teremos:
y - yo = mr(x - xo), onde:
yo = 3
xo = 0
mr = 2
Portanto,
y - yo = mr(x - xo), onde:
y - 3 = 2(x - 0)
y - 3 = 2x
y = 2x + 3
ALTERNATIVA B
Próxima Aula
Aula Anterior
Página do Capítulo
Página do Curso
Página Principal