Ângulo Entre Duas Retas - Parte II

Casos Especiais:

- quando uma das retas é vertical:



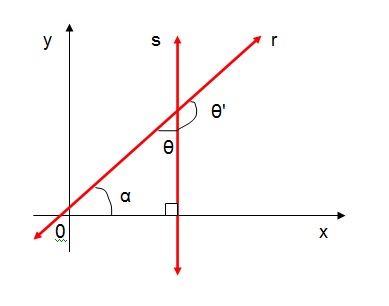
Temos que:

θ + α = 90^o

Isolando θ

θ = 90^o - α
tg θ = tg(90^o - α) (aplicando tg em ambos os lados)
tg θ = cotg α
tg θ = (1/tg α)

Fazendo tg θ = m_r (conforme gráfico), temos:

tg θ = (1/tg α)
tg θ = (1/m_r)

Para que o ângulo θ seja agudo, fazemos:



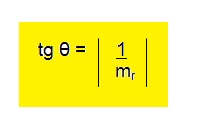
- quando as retas são perpediculares:



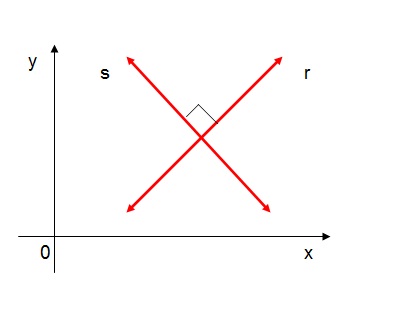
Nesta situação, o ângulo entre as retas vale 90^o. Por isso, não é conveniente usar a fórmula da tangente, pois o ângulo vale 90^o e a tangente deste ângulo não existe.

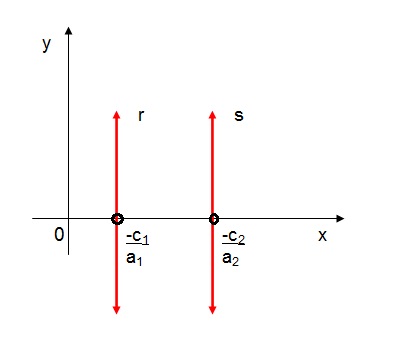
- quando as retas são da forma ax + c = 0:

Neste caso, as retas são verticais e paralelas. Logo, não há coeficiente angular das retas. Portanto, θ = 0^o.



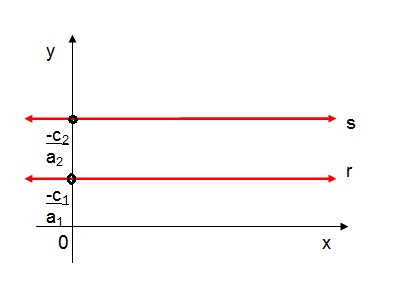
- quando as retas são da forma by + c = 0:

Nesta situação, o ângulo entre as retas vale 0^o. As retas são paralelas e horizontais entre si.

Exercício:

(VUNESP) Calcule o ângulo agudo formado pelas retas y = 2 e x - y - 1 = 0.

Solução:

Vamos defiinir as retas da seguinte forma:

r: y = 2
s: x - y -1 = 0

Como y = 2 é uma reta horizontal seu coeficiente angular é zero. Logo, m_r = 0.

Na equação x - y - 1 = 0, temos:

a = 1
b = -1

Logo,

m_s -(a/b) = -(1/(-1)) = -(-1) = 1

Logo, m_s = 1.

Usando a fórmula da tangente:

Próxima Aula

Aula Anterior

Página do Capítulo

Página do Curso

Página Principal