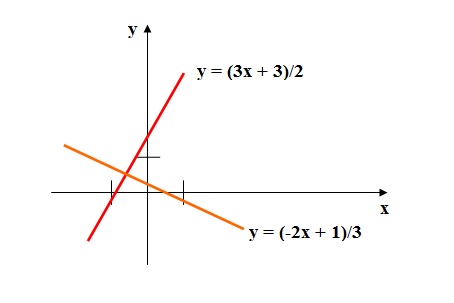Função

Vamos resolver uma questão envolvendo função do vestibular da FUVEST 2001 - 1ª fase.

A questão é:



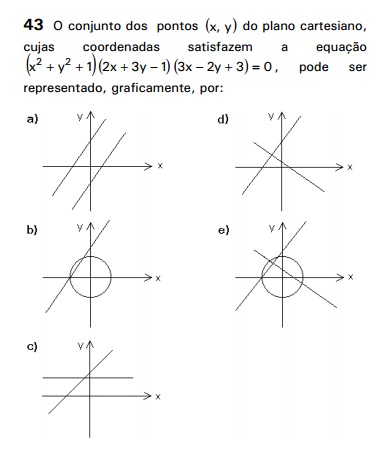
Nesta questão, nós temos a multiplicação de três equações cujo resultado é igual a zero.

Logo,

x² + y² + 1 = 0
2x + 3y - 1 = 0
3x - 2y + 3 = 0

A equação x² + y² + 1 = 0 não tem solução real, pois resulta numa circunferência de raio negativo:

x² + y² = -1.

Então, no gráfico teremos as duas retas:

2x + 3y - 1 = 0
3x - 2y + 3 = 0

Trabalhando com 2x + 3y - 1 = 0, teremos:

2x + 3y - 1 = 0
3y = -2x + 1
y = (-2x + 1)/3

Para x = 0, teremos:

y = 1/3

Para y = 0, teremos:

0 = (-2x + 1)/3
0 = -2x + 1
-1 = -2x
2x = 1
x = 1/2

Então, para a primeira função, teremos os pontos (0,1/3) e (1/2,0).

Trabalhando com 3x - 2y + 3 = 0, teremos:

3x - 2y + 3 = 0
-2y = -3x - 3
2y = 3x + 3
y = (3x + 3)/2

Para x = 0, teremos:

y = 3/2

Para y = 0, teremos:

0 = (3x + 3)/2
0 = 3x + 3
-3 = 3x
3x = -3
x = -3/3
x = -1

Então, para a segunda função, teremos os pontos (0,3/2) e (-1,0).

Com os pontos da primeira e segunda função, esboçaremos o gráfico:



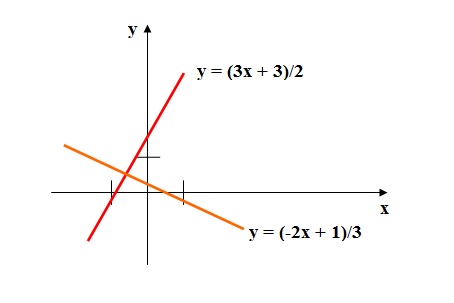
A alternativa que melhor representa a alternativa acima é a:

ALTERNATIVA D

---

Questão Anterior

Página Principal

Questão Posterior