Trigonometria
Vamos resolver agora uma questão envolvendo trigonometria do vestibular da FUVEST 2001 - 1ª fase.

A questão é:


Na figura abaixo, vamos esquematizar os dados da questão:



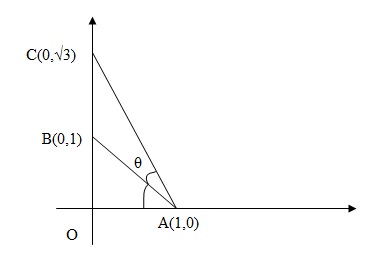
Vamos primeiro trabalhar com o triângulo Δ OAB

A tangente do ângulo OÂB vale:

tg (OÂB) = (cateto oposto/cateto adjacente)
tg (OÂB) = 1/1
tg (OÂB) = 1

Se tg (OÂB) = 1, então o ângulo OÂB vale:

OÂB = 45º

Agora vamos trabalhar com o triângulo Δ OAC.

A tangente do ângulo OÂC vale:

tg (OÂC) = (cateto oposto/cateto adjacente)
tg (OÂC) = √ 3/1
tg (OÂC) = √ 3

Se tg (OÂC) = √ 3, então o ângulo OÂC vale:

OÂC = 60º

Por fim, vamos trabalhar com o triângulo Δ BAC.

O valor do ângulo BÂC vale:

BÂC = OÂC - OÂB
BÂC = 60º - 45º
BÂC = 15º

ALTERNATIVA E


Página Principal

Questão Posterior