

Geometria Plana
Vamos resolver uma questão envolvendo geometria plana do ENEM 2013.
A questão é:

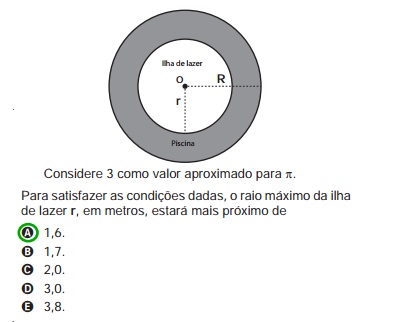
O volume do cilindro é dado por:
V = π . r2 . h
Nesta questão nós temos 3 volumes a considerar:
V1 = volume total (ilha de lazer + piscina)
V2 = volume da ilha de lazer
V3 = volume da piscina
O volume a ilha de lazer é dado por:
V2 = π . r2 . h
Onde,
r = r
h = 1m
π = 3 (aproximado)
Portanto,
V2 = π . r2 . h
V2 = 3 . r2 . 1
V2 = 3 . r2
O volume da piscina é dado por:
V3 = π . r2 . h
Conforme a questão, o valor mínimo do volume da piscina é:
V3 = 4m3
O volume total é dado por:
V1 = V2 + V3
Mas conforme a questão, V1 = 12m3
Então,
V1 = V2 + V3
12m3 = 3r2 + 4m3
12m3 - 4m3 = 3r2
8m3 = 3r2
3r2 = 8m3
r2 = (8m3)/3
r = √ 8m3 / 3
r = √ 2,66m3
r = 1,632m
Portanto, o valor do raio r é próximo de 1,6m
ALTERNATIVA A
Questão Anterior
Página Principal
Questão Posterior





