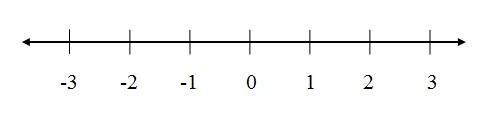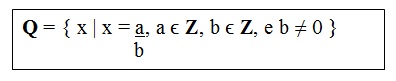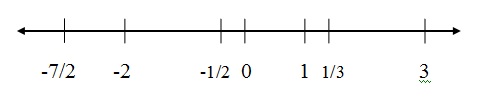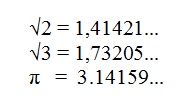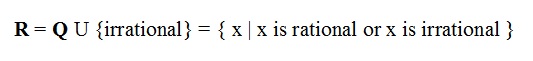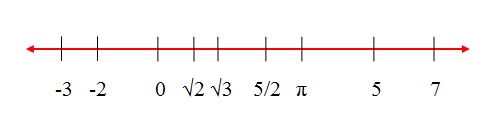Chapter 1
Section 1.6
Numerical sets
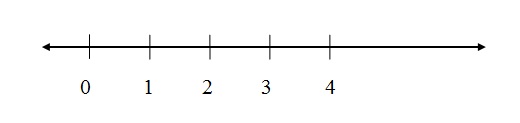
Sets of Natural Numbers
Representation: N = {0, 1, 2, 3, 4, 5, ...}
Subset:
A very represented subset of the natural numbers is one where the zero element does not exist.
The letter N is accompanied by an asterisk (*).
Example:
N * = {1, 2, 3, 4, 5, ...}
Graphic representation:
Whole Number Sets
Representation: Z = {...- 5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}
Subset:
A well-represented subset of integers is one where zero is not present.
The letter Z is marked with an asterisk (*).
Example:
Z * = {..., - 3, -2, -1, 1, 2, 3, ...}
Another example is the subset of nonnegative integers.
Representation:
Z + = {0, 1, 2, 3, ...}
Finally, there is also the subset of non-positive integers.
Representation:
Z_ = {...- 3, -2, -1, 0}
Graphic representation of the set of integers:
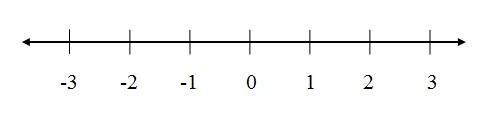
Sets of Rational
Definition:
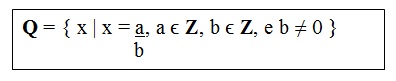
Examples:
3/4, 5/6, 7/8, 11/5, -3, 2, 0, 7.
Every rational number can be written in the form a / b.
Examples:
A) -3 = -3/1
B) 0 = 0/10
Rational numbers are divided into exact or finite decimals.
Examples:
A) 2/5 = 0.4
B) 100/25 = 4
Periodic or infinite decimals
Examples:
A) 1/3 = 0.333 ...
B) 10/3 = 3.333 ...
Graphical representation of the rational set:
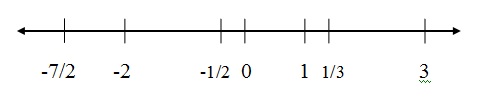
Sets of Irrational Numbers
Irrational numbers are those that can not be represented as a / b (rational)
Examples:
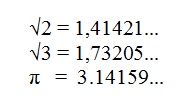
Irrational numbers form non-periodic tithe.
Graphic representation:

Real Number Sets
Definition:
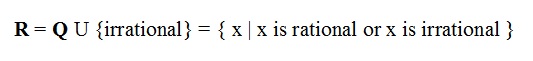
Venn diagram for the set of real numbers:
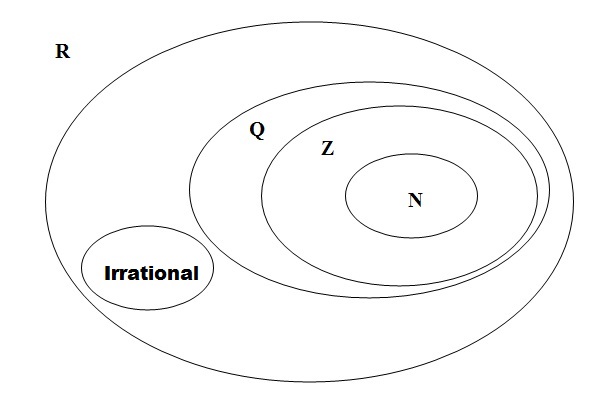
Subassemblies of the real numbers:
A) R * = R - (0)
B) R + = set of non-negative real number
s
C) R_ = set of non-positive real numbers
Graphic representation:
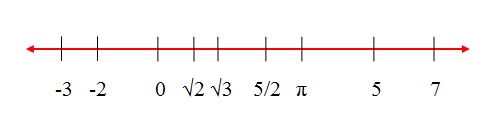
The real numbers fill all the points of the straight line above. Therefore, this line is called the real line.
Previous Class
Course Page
Next Class