Soma dos N Termos de Uma P.G. Infinita

Capítulo 9

Seção 9.5

A soma dos "n" termos de uma P.G. infinita é dada pela seguinte fórmula:


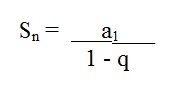
Onde:

S_n é a soma dos n termos.
a₁ é o primeiro termo.
q é a razão
q deve estar entre 0 e 1. (0 < q < 1)

Exemplo:

a) Encontre a soma da P.G. infinita , (2, 1, 1/2, 1/4,...) vale:

Resolução:

Para resolvermos essa questão, fazemos uso da fórmula da soma dos n termos de uma P.G. infinita.

Dados:

S_n = ?
q = 1/2
a₁ = 2

Substituindo na fórmula da soma dos n termos de uma P.G. infinita, teremos:

S_n = 2/(1 - 1/2)
S_n = 2/(1/2)
S_n = 4

Portanto, a soma da P.G. infinita vale S_n = 4

b) Encontre a fração geratriz da dízima periódia 0,42333...

O número 0,42333... é igual a 0,42 + 0,003 + 0,0003 + 0,00003...

Em forma de fração, a soma fica: 42/100 + 3/1000 + 3/10000 + 3/100000 + ...

Observe que o primeiro número dessa soma, o número 0,42, é diferente dos outros termos. Então, vamos deixar este número de lado por enquanto e vamos trabalhar com os termos restantes.

3/1000 + 3/10000 + 3/100000 + ... constitui uma soma infinita de uma P.G. Portanto, vamos usar a fórmula da soma dos n termos para encontrar
o valor da soma.

Dados:

S_n = ?
q = (3/10000)/(3/1000) = 1/10
a₁ = 3/1000

Substituindo na fórmula da soma dos n termos, teremos:

S_n = (3/1000)/(1 - 1/10) = (3/1000)/(0,9) = 1/300

Agora para acharmos a fração geratriz, devemos somar 1/300 com 42/100, aquele número que deixamos de lado no início do exemplo.

Logo, a fração geratriz dessa dízima periódica será: 1/300 + 42/100 = 127/300.

A fração geratriz é 127/300.