Forma Trigonométrica Ou Polar de Um Número Complexo

Capítulo 15

Seção 15.11

Veja o gráfico no plano de Argand-Gauss abaixo:



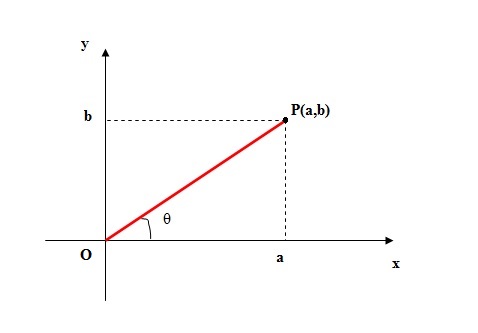
Na aula passada, vimos que:



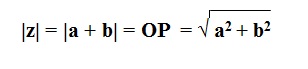
Vimos também que:

sen θ = b/OP = b/|z|
cos θ = a/OP = a/|z|

Logo,
sen θ = b/|z| => b = |z|.sen θ
cos θ = a/|z| => a = |z|.cos θ

Sabemos que a forma algébrica do número complexo é:

z = a + bi

Fazendo as substituições:

z = |z|.cos θ + |z|(sen θ)i
z = |z|(cos θ + sen θ i)

Portanto, a forma trigonométrica de um número complexo é:

z = |z|(cos θ + sen θ i)

Exercício:

1) Transforme da forma trigonémetrica para algébrica o número complexo z = 2(cos π /4 + (sen π /4).i)

Resolução:

Conforme a tabela trigonométrica:

cos π /4 = √ 2/2
sen π /4 = √ 2/2

Então,

z = 2( √ 2/2 + ( √ 2/2).i)
z = 2( √ 2/2(1 + i))
z = √ 2(1 + i)
z = √ 2 + √ 2.i

Portanto, a forma algébrica de z = 2(cos π /4 + (sen π /4).i) será:

z = √ 2 + √ 2.i