Módulo e Argumento de Um Número Complexo

Capítulo 15

Seção 15.10

Veja o gráfico no plano de Argand-Gauss abaixo:



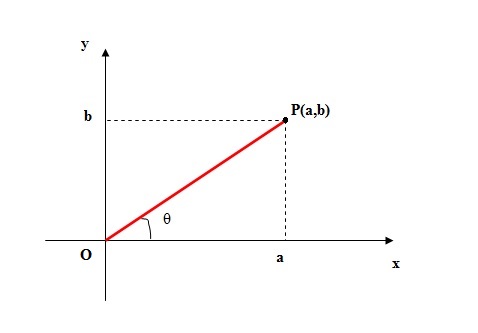
Usando Pitágoras:



O módulo de z é o valor da reta OP. Então,



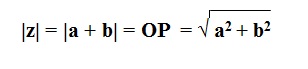
O argumento é a medida do ângulo θ sempre no sentido anti-horário e ele deve estar sempre entre 0 < θ < 2 π.

Notação:

θ= arg(z)

Temos também que:

sen θ = b/OP
cos θ = a/OP

Exercício:

Calcule o módulo, o argumento do número complexo z = 1 + raiz 3i.

Resolução:

Portanto, o módulo do número complexo vale |z| = 2.

O argumento será:

sen θ = b/OP
cos θ = a/OP

sen θ = b/|z|
cos θ = a/|z|

Então,

sen θ = √ 3/2
cos θ = 1/2

Pela tabela trigonométrica, o valor de θ será:

θ = π / 3