
A Pirâmide

Definição:
A pirâmide é um poliedro que possui uma base que tem um polígono com um formato qualquer e cujas faces laterais são triângulos que tem um vértice em comum.
Elementos de uma pirâmide

base - polígono convexo Q
altura h - vai do plano da base π até o vértice V.
faces laterais - áreas dos triângulos; a quantidade de faces é determinada pelas quantidades de arestas da base.
Classificação de triângulos
Quando a projeção ortogonal coincide com o centro do polígono, dizemos que a pirâmide é reta.
Quando a pirâmide reta possui uma base cujo polígono é regular, dizemos que a pirâmide é regular.
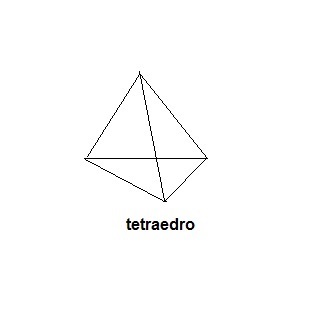
Tetraedro
Quando a base da pirâmide é triangular dizemos que a pirâmide é um tetraedro.
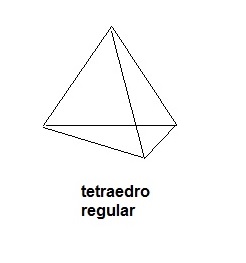
Tetraedro Regular
Quando todas as faces do tetraedro forem triângulos equiláteros, dizemos que o tetraedro é regular.
Relação entre os elementos de uma pirâmide regular
Seja uma pirâmide regular hexagonal de aresta lateral s e aresta da base a:
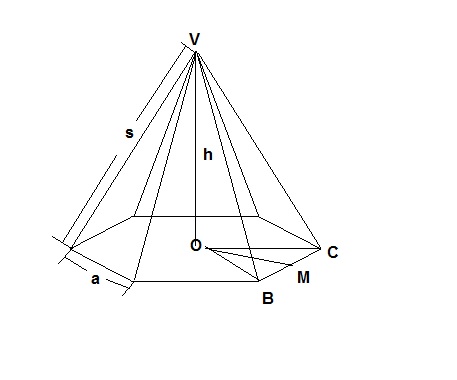
MC = a/s
h2 = s2 - a2
- base da pirâmide regular:
A base da pirâmide pode ser inscrita num círculo de raio OB = R.

- apótema da base:

- face lateral:
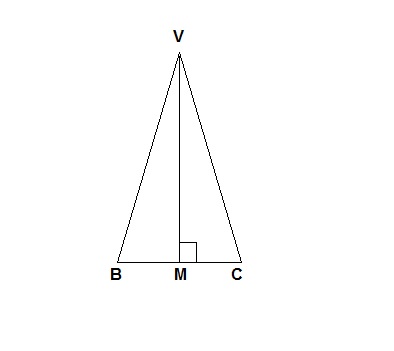
A face lateral da pirâmide é um triângulo isósceles. A reta VM é o apótema da pirâmide.
- triângulos VOB e VOM:

Os triângulos VOB e VOM são retângulos.
Áreas da pirâmide
- área lateral (AL) - soma de todas as áreas laterias da pirâmide.
- área base (AB) - área da base da pirâmide (polígono convexo).
- área total (AT) - soma da área da base com as áreas laterais.
AT = AB + AL
No caso de uma pirâmide regular:
AL = n.(a.g/2)
AB = p.ap
onde:
a é a aresta da base
g é o apótema da pirâmide
n é o número de arestas laterais
p é o semiperímetro da base
ap é o apótema do polígono da base
Volume
O volume de uma pirâmide é dado por:
VPIRÂMIDE = (1/3).AB.h
Exercício:
(MACK-SP) - Uma pirâmide cuja base é um quadrado de lado 2a tem o mesmo volume que um prisma cuja base é um quadrado de lado a. A razão entre as alturas da pirâmide e do prisma, nessa ordem, é:
a) 3/4
b) 3/2
c) 1/4
d) a/3
e) 3a
Solução:
Temos que:
VPIRÂMIDE = VPRISMA
(1/3).AB.hPIRÂMIDE = AB.hPRISMA
(1/3).(2a)2.hPIRÂMIDE = a2.hPRISMA
(1/3).4a2.hPIRÂMIDE = a2.hPRISMA
(hPIRÂMIDE/hPRISMA) = (3.a2)/4a2
(hPIRÂMIDE/hPRISMA) = 3/4
ALTERNATIVA A
Próxima Aula
Aula Anterior
Página do Capítulo
Página do Curso
Página Principal