Posições de retas no plano e no espaço

Reta pertencente a um plano

- se uma reta possui dois 2 pontos dentro de um plano, então esta reta está contida neste plano.



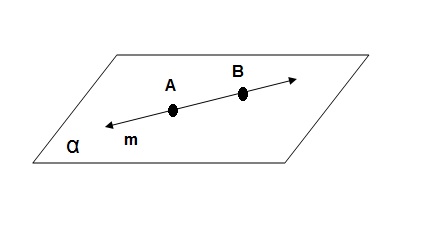
A ∈ α e B ∈ α
A ∈ m e B ∈ m

Logo,

m ⊂ α

Reta concorrente ou incidente ao plano

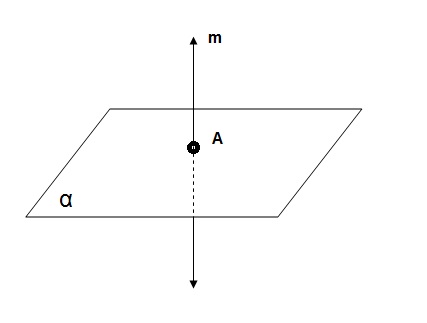
Quando uma reta m atravessa um plano α ou que m e α são concorrentes em A quando m ∩ α = |A|.

Reta paralela ao plano

Se uma reta m e um plano α não têm ponto em comum, então a reta m é paralela a uma reta n contida no plano α. Logo, m // α. Há infinitas retas paralelas, reversas ou ortogonais a m no plano α.

Axioma:

"Quando dois planos distintos têm um ponto em comum, então a sua intersecção é dada por uma única reta que passa por esse ponto."

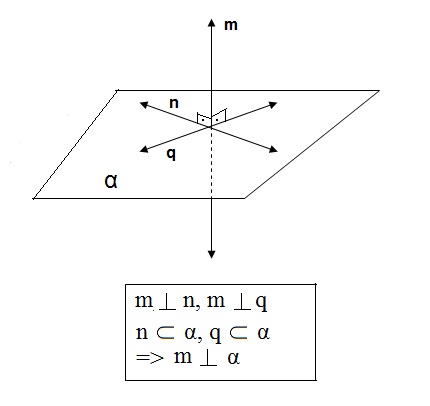
Plano e reta: perpendicularismo

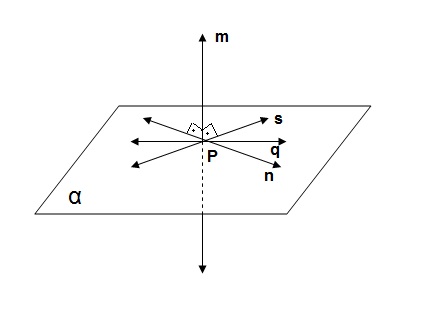
Uma reta m será perpendicular a um plano α se, e somente se, é perpendicular as infinitas retas de α que passam pelo ponto A que é a intersecção de m e α.

Observações:

- quando uma reta m é perpendicular a um plano α , então ela será perpendicular ou ortogonal a toda reta contida em α.



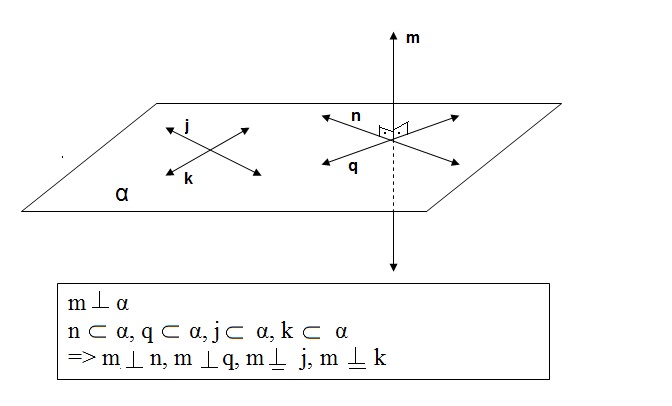
- uma reta m perpendicular a duas retas concorrentes contida em α será também perpendicular ao plano α.

Próxima Aula

Página do Capítulo

Página do Curso

Página Principal