Paralelismo e Concorrência Entre Retas

Paralelismo

Definição:

Sendo r e s duas retas distintas e que não são verticais. Quando o coeficiente angular de ambas são iguais. dizemos que as retas são paralelas.

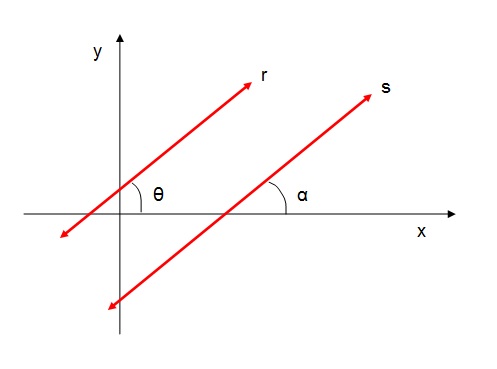
Notação:

O símbolo para retas paralelas é //.

Demonstração

r // s ⇔ θ = α ⇔ tg θ = tg α ⇔ m_r = m_s

Logo,

r // s ⇔ m_r = m_s

Observação:

Concorrência

Definição

Quando os coeficentes de duas retas r e s forem diferentes elas são concorrentes.

r e s concorrentes => m_r ≠ m_s => -(a₁/b₁) ≠ -(a₂/b₂)

Exemplo:

1) Sejam as retas:

r: 2x - 3y + 1
s: 4x -y + 2

Verifique se r e s são concorrentes:

Solução

Dados:

reta r:
a₁ = 2
b₁ = -3

a₂ = 4
b₁ = -1

Então,

m_r = -(a₁/b₁)
m_r = -(2/(-3)) = 2/3

m_s = -(a₂/b₂)
m_s = -(4/(-1)) = 4

Logo, m_r ≠ m_s. Portanto, r e s são concorrentes.

Exercício:

1) (PUC-RS) A equação da reta que passa pelo ponto P(2,5) e é paralela à reta de equação x - y + 2 = 0 é:

a) 3x - 2y + 4 = 0
b) 2x - 3y + 11 = 0
c) x - y + 7 = 0
d) x - y + 3 = 0
e) x - y - 3 = 0

Solução:

Temos as retas:

r: que passa pelo P(2,5)
s: x - y + 2 = 0

As retas r e s têm o mesmo coeficiente angular já que são paralelas. Logo.

m_r = m_s
m_r = -(a₂/b₂)
m_r = -(1/(-1))
m_r = 1

Logo, o coeficiente angular de r é igual a m_r = 1

Sabemos que y - y_o = m_r(x - x_o)

onde:

m_r = 1
y_o = 5 (coordenada y do ponto P)
x_o = 2 (coordenada x do ponto P)

Logo,

y - y_o = m_r(x - x_o)
y - 5 = 1.(x - 2)
y - 5 = x - 2
y - 5 - x + 2 = 0
-x + y - 3 = 0
x - y + 3 = 0 (multiplicando por -1)

Logo, a equação da reta que passa pelo ponto P(2,5) é x - y + 3 = 0

ALTERNATIVA D

Próxima Aula

Aula Anterior

Página do Capítulo

Página do Curso

Página Principal