Perpendicularismo

Definição:

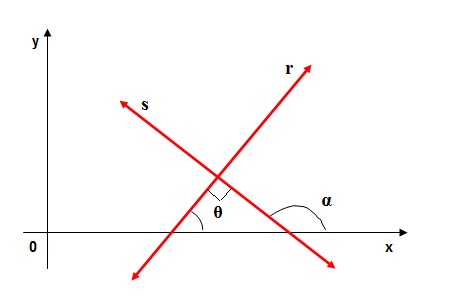
Sendo r e s, duas retas que não são verticais. Quando o produto do coeficiente angular de ambas é igual a -1, dizemos que as retas são perpendiculares.

m_s.m_r = -1

Notação:

O símbolo para retas perpendiculares é ┴.

Demonstração

Pelo teorema do ângulo externo, temos:

α = 90^o + θ

Aplicando tg em ambos os membros da igualdade:

tg α = tg 90^o + tg θ => tg α = [sen (90^o + θ)]/[cos (90^o + θ)]
tg α = (cos θ)/(-sen θ) => tg α = -cotg θ => tg α = -(1/tg α) => tg α.tg θ = -1

Temos que:

m_s = tg α
m_r = tg θ

Então,

tg α.tg θ = -1
m_s.m_r = -1

Propriedade:

- Sendo r e s duas retas perpendiculaes não-verticais. O coeficiente angular de r é o inverso do coeficiente angular de s com o sinal trocado.

m_s =  -1
          m_r

Exercício

1) (FUVEST) No plano cartesiano, são dados os pontos A(-1,2), B(1, 3) e C(2,-1). Determine a equação da reta que passa por C e é perpendicular a AB.

a) 2x + y - 3 = 0
b) 2x - y - 3 = 0
c) 2x - y - 7 = 0
d) x + 2y - 3 = 0
e) x - 2y - 3 = 0

Solução:

A equação geral da reta AB é:



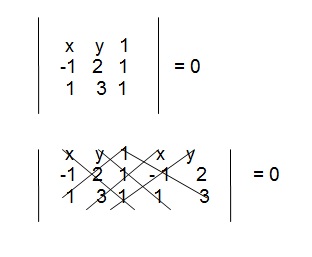
x.2.1 + y.1.1 + 1.(-1).3 - (1.2.1 + 3.1.x + (1.(-1).y) = 0
2x + y - 3 - (2 + 3x - y) = 0
2x + y - 3 - 2 - 3x + y = 0
2y - x - 5 = 0 (equação geral)

Isolando y:

2y - x - 5 = 0
y = (1/2)(x + 5)

Coeficiente angular da reta AB: m_AB = 1/2
Coeficiente angular de reta que passa por C: m_C = -2 (inverso com sinal trocado, retas perpendiculares)

Temos a equação y - y_C = m_C(x - x_C)

Dados:

y_C = -1
x_C = 2
m_C = -2

Logo, a equação será:

y - y_C = m_C(x - x_C)
y + 1 = (-2)(x - 2)
y + 2x + 1 - 4 = 0
y + 2x - 3

A equação da reta será:

2x + y - 3 = 0

ALTERNATIVA A

Próxima Aula

Aula Anterior

Página do Capítulo

Página do Curso

Página Principal