
Equação Geral da Reta
A equação geral da reta é dado por:
ax + by + c
Demonstração:
Seja uma reta r, e três pontos A(xA, yA) e B(xB, yB) e P(x,y) (ponto genérico).
Estando os três alinhados, teremos:
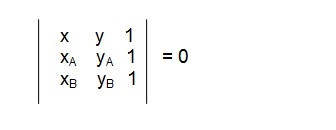
Teremos:
-xByA - xyB -yxA + xyA + yxB + xAyB = 0
(yA - yB)x + (xB - xA)y + (xAyB - xByA) = 0
Chamando de:
a = yA - yB
b = xB - xA
c = xAyB - xByA
Logo,
(yA - yB)x + (xB - xA)y + (xAyB - xByA) = 0
ax + by + c = 0
Propriedades:
Seja P(m.n) um ponto genérico:
- se am + bn + c = 0, P é ponto da reta.
- se am + bn + c ≠, P não é ponto da reta.
Exercícios:
(VUNESP-SP) A reta que passa pelos pontos (2, 1/2) e (0, 5/2) tem equação:
a) x = y
b) x - y = 1
c) 2x + 2y - 5 = 0
d) x + y = 1
e) x - y - 2 = 0
Solução:
Dados:
xA = 2
yA = 1/2
xB = 0
yB = 5/2
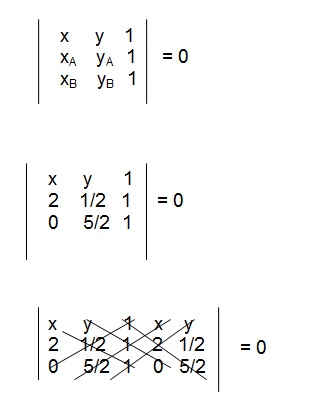
Então,
x.(1/2).1 + y.1.0 + 1.2.(5/2) - 0.(1/2).1 - (5/2).1.x - 1.2.y = 0
x/2 + 0 + 5 - 0 - (5/2).x - 2y = 0
x/2 + 5 - (5/2)x - 2y = 0
x + 10 - 5x - 4y = 0 (multiplicando por 2)
-4x - 4y + 10 = 0
-2x - 2y + 5 = 0 (dividindo por 2)
2x + 2y - 5 = 0 (multiplicando por -1)
Portanto, a equação da reta é:
2x + 2y - 5 = 0
ALTERNATIVA C
Próxima Aula
Aula Anterior
Página do Capítulo
Página do Curso
Página Principal