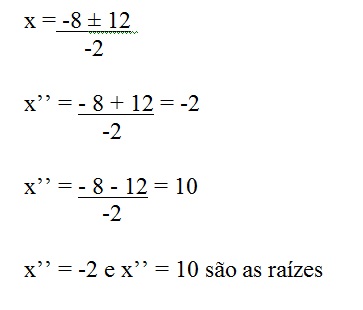Vértice de uma parábola
Hoje iremos fazer uma questão envolvendo vértice de uma parábola do vestibular da FUVEST 2020 - 1a. fase.
A questao é :

A questão se trata de uma funcão. Vamos chamar de x a variacão de cada R$ 1,00 a menos no preco do combo e de y o valor arrecadado pelas vendas:
y(x) = (10 - x).(200 + 100.x)
Análise da funcão:
O fator (10 - x) refere-se ao valor de cada combo. Já o fator (200 + 100.x) refere-se a quantidade de combos vendidos.
Temos que:
y(x) = (10 - x).(200 + 100.x)
y(x) = 2000 + 1000x - 200x - 100x2
y(x) = 2000 + 800x - 100x2
Agora, iremos encontrar as raízes da questão. Para facilitar nossos cálculos, vamos dividir toda a funcão por 100 e igualar a zero.
y(x) = 2000 + 800x - 100x2
0 = 20 + 8x - x2
- x2 + 8x + 20 = 0
Temos que:
a = -1
b = 8
c + 20

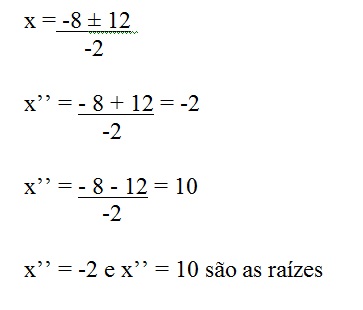
Fazendo um esboco do gráfico temos:

O valor máximo de vendas encontra-se no vértice da parábola. Portanto, devemos encontrar primeiro a coordenada x do vértice.
Logo, xv = -b/2a
xv = -b/2a
Mas,
b = 8
a = -1
Então,
xv = -b/2a
xv = -8/-2
xv = 4
Substituindo x = 4 na funcão y(x), descobrimos o valor máximo arrecadado:
y(x) = (10 - x).(200 + 100.x)
y(4) = (10 - 4).(200 + 100.4)
y(4) = 6.(200 + 400)
y(4) = 6.600
y(4) = 3600
Portanto, o maior valor arrecadado foi de R$ 3.600,00
ALTERNATIVA D
Questão Anterior
Pagina Principal
Questão Posterior