
Geometria Plana
Vamos resolver uma questão envolvendo geometria plana do vestibular da FUVEST 2006 - 1ª fase.
A questão é:
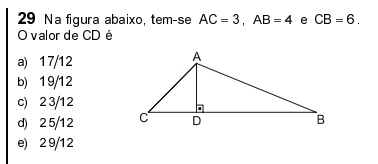
Vamos redesenhar a figura:

Aplicando Pitágoras no triângulo ADC, teremos:
42 = y2 + z2
16 = y2 + z2
z2 = 16 - y2
Aplicando Pitágoras no triângulo ABD, teremos:
32 = x2 + z2
9 = x2 + z2
z2 = 9 - x2
Temos que:
z2 = 16 - y2
z2 = 9 - x2
Logo,
16 - y2 = 9 - x2
x2 - y2 = -7
A questão nos diz que CB = 6
Mas CB = x + y
Portanto,
x + y = 6
Teremos então o seguinte sistema:
x2 - y2 = -7
x + y = 6
Vamos trabalhar com a equação:
x + y = 6
Isolando x, teremos:
x = 6 - y
Substituindo em x2 - y2 = -7:
x2 - y2 = -7
(6 - y) 2 - y2 = -7
36 - 12y + y2 - y2 = -7
36 - 12y = -7
-12y = -7 - 36
-12y = -43
y = 43/12
Temos que:
x + y = 6
Logo,
x + y = 6
x + 43/12 = 6
x = 6 - 43/12
x = (72 - 43)/12
x = 29/12
Pela figura, vemos que BD = x.
Portanto,
BD = 29/12
ALTERNATIVA E
Página Principal
Questão Posterior



