Logaritmos


Vamos resolver uma questão envolvendo logaritmo do vestibular da FUVEST 2003 - 1ª fase.

A questão é:



Vamos ver as condições de existência (C.E.)

O termo (3x + 4) e (2x - 1) devem ser maiores que zero, pois ambos são logaritmandos.

Logo,

3x + 4 > 0 => 3x > -4 => x > -4/3
2x - 1 > 0 => 2x > 1 => x > 1/2

Da intersecção destas duas desigualdades, temos que x > 1/2 => conjunto A

Temos que f(x) = log₃(3x + 4) - log₃(2x - 1) = log₃[(3x + 4)/(2x - 1)]

A questão nos diz que f(x) > 1. Logo,

f(x) = log₃[(3x + 4)/(2x - 1)]
log₃[(3x + 4)/(2x - 1)] > 1
[(3x + 4)/(2x - 1)] > 3
3x + 4 > 3.(2x - 1)
3x + 4 > 6x - 3
3x - 6x > -3 - 4
-3x > -7
3x < 7
x < 7/3

Observe também que o denominador (2x - 1) deve ser maior que zero. Portanto,

2x - 1 > 0
2x > 1
x > 1/2

Logo, para f(x) > 1, teremos 1/2 < x < 7/3 => conjunto B

Por fim, os valores de x para os quais f está definida e onde f(x) > 1 está na intersecção do conjunto A com B. Logo,


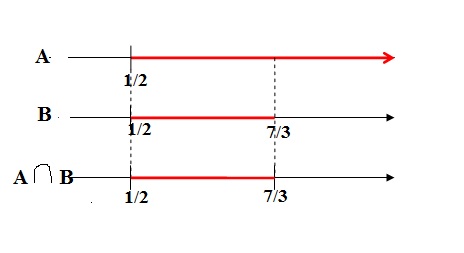
A ∩ B = 1/2 < x < 7/3

ALTERNATIVA C

---

Questão Anterior

Página Principal

Questão Posterior