Fórmula de Moivre - Potenciação de Números Complexos na Forma Trigonométrica

Capítulo 15

Seção 15.13

A fórmula de Moivre é dada por:

zⁿ = |z|ⁿ.(cos n. θ + i.sen n. θ )

O número complexo é elevado a potência n. Esta também multiplica os argumentos, sendo que o módulo também está elevado a n.

Exercício:

1) Sendo z = [ √ 2/2 + ( √ 2/2).i], calcule z⁶:

Vamos calcular primeiro o módulo:



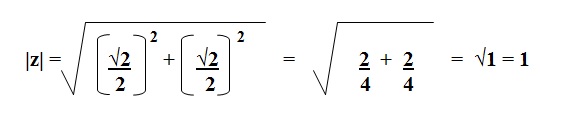
Agora vamos calcular θ:

cos θ = a/|z| = ( √ 2/2)/1 = √ 2/2
sen θ = b/|z| = ( √ 2/2)/1 = √ 2/2

Portanto, θ = π /4

Sabemos que:

z = |z|(cos θ + i.sen θ). Então,

z = 1.(cos π / 4 + i.sen (π /4))

Portanto, z⁶ será:

z⁶ = 1⁶.(cos 6.(π / 4) + i.sen 6.(π /4))
z⁶ = (cos 3.(π / 2) + i.sen 3.(π /2))
z⁶ = 0 + (-i)
z⁶ = -i

Portanto, z⁶ = -i