
Coeficiente Angular
Definição
Seja o ângulo θ. O coeficiente angular da reta é o número real m tal que:
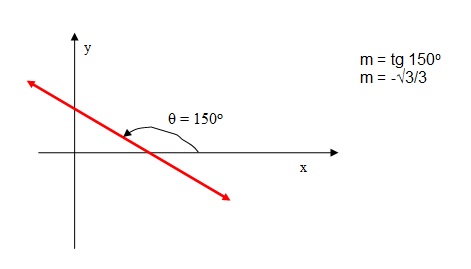
m = tg θ, θ = 90o
Propriedades:
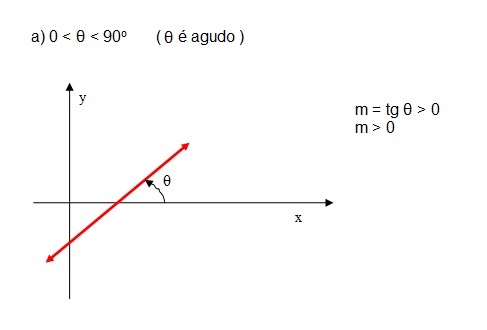

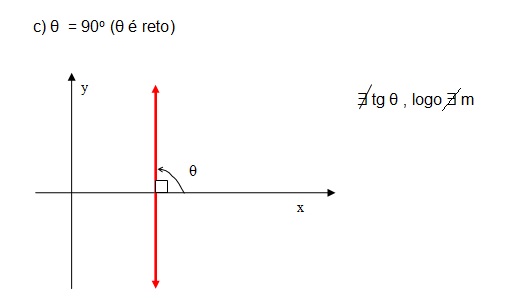
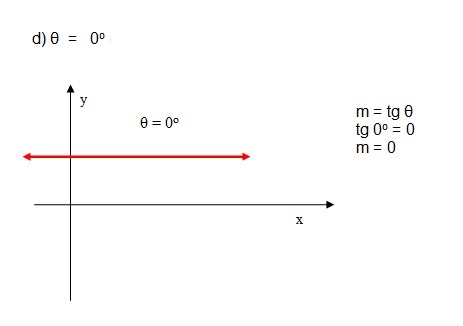
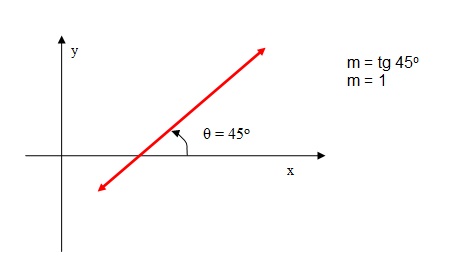
Determinação do coeficiente angular:
- quando o ângulo θ é conhecido:
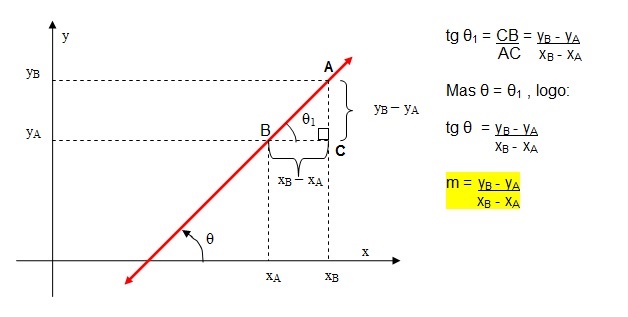
- quando as coordenadas de dois pontos distintos de uma reta são conhecidas A(xa,ya) e B(xb,yb).
- quando a equação geral da reta é conhecida:
Da aula de equação geral da reta, demonstramos que m = -a/b.
Exemplo:
1) Dada a reta 6x - 2y + 5 = 0, qual é o valor do coeficiente angular ?
Solução:
Dados:
a = 6
b = -2
Logo, mr = -(a/b) => mr = -(6/(-2)) => mr = 3
Descobrindo uma equação geral da reta r com coeficiente angular e um ponto conhecidos.
Sendo P(xo,yo) e Q(x,y) e que P ≠ Q, temos que:
m = -(a/b)
onde,
a = yo - y
b = xo - x
Logo,
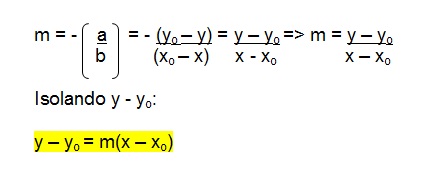
Exercício:
(PUC-SP) A equação da reta com coeficiente angular m = -4/5 que passa pelo P(2,-5) é:
a) 4x + 5y + 12 = 0
b) 4x + 5y + 14 = 0
c) 4x + 5y + 15 = 0
d) 4x + 5y + 17 = 0
e) n.d.a
Solução:
Temos que:
y - yo = m(x - xo)
Dados:
xo = 2
yo = -5
m = -4/5
Logo,
y - yo = m(x - xo)
y - (-5) = (-4/5)(x - 2)
y + 5 = (-4/5)(x - 2)
y + 5 = (-4/5)(x) + 8/5
(4/5)x + y + 5 - 8/5 = 0
(4/5)x + y + 17/5 = 0
4x + 5y + 17 = 0 (multiplicando tudo por 5)
Logo, a equação da reta é: 4x + 5y + 17 = 0
ALTERNATIVA D
Próxima Aula
Aula Anterior
Página do Capítulo
Página do Curso
Página Principal